Générer une surface mathématique
Certaines formes peuvent êtres décrites par des formules mathématiques : les positions dans l'espace de chaque point de la forme sont traduits par une seule formule, dont on fait varier un certain nombre de paramètres.
Choisir une forme
Il existe un très grand nombre de surfaces mathématiques simples, et leur formule est souvent facilement trouvable sur internet. Il y en a un certain nombre à cette adresse : http://local.wasp.uwa.edu.au/~pbourke/geometry . Attention, certaines formules ne sont pas traduites, et certaines peuvent être redoutables.
Je vais prendre comme exemple le ruban de Möbius. C'est un objet mathématique très simple mais que j'aime beaucoup, sa principale caractéristique étant d'être la seule surface “complexe” n'ayant… qu'un seul côté ! Suivez mentalement sa face, vous parcourez toute la surface de l'objet. Un petit tour sur Wikipedia m'a indiqué sa formule. Cette dernière donne trois équations correspondant aux coordonnées x, y et z de tous les points de la surface :
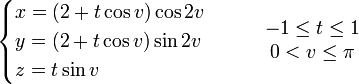
De la formule aux points
Bases
Pour commencer écrivons les formules données pour x, y et z en Python :
# on utilise des formules de math (cos, sin...) # donc on importe le module from math import * x = (2 + t * cos(v)) * cos(2 * v) y = (2 + t * cos(v)) * sin(2 * v) z = t * sin(v)
Si nous lançons le code maintenant nous avons une belle erreur : c'est bien beau d'utiliser des variables t et v, mais quelle sont leurs valeurs? Il nous est indiqué, à droite des formules de Wikipédia, leurs intervalles : c'est toutes les valeurs qu'elles prennent pour créer le ruban.
t doit prendre différentes valeurs comprises entre -1 et 1, hors c'est exactement ce que permet une boucle :
#affiche les valeurs de t de -1 à 1, tous les 0.2 t = -1.0 while t <= 1.0 : print t, t += 0.2
-1.0 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1.0
Si l'on incrémente t d'une toute petite valeur il prendra un très grand nombre de valeurs avant d'arriver à 1; si au contraire on incrémente d'une grande valeur la boucle ne fera que très peu de tours.
Comprendre v et t
Pour se représenter le rapport entre le code et un objet 3D, nous allons créer de tout petit polyCubes pour représenter chaque point que nous calculons :
# on va utiliser des commandes Maya # donc on importe le module import maya.cmds as mel from math import * v = 0 #valeur fixe de v t = -1.0 #valeur minimum de t while t <= 1.0 : #valeur maximum de t # on calcule les coordonnées des points x = (2 + t * cos(v)) * cos(2 * v) y = (2 + t * cos(v)) * sin(2 * v) z = t * sin(v) # on place un polyCube selon ces coordonnées mel.polyCube(h=0.1, w=0.1, d=0.1) mel.move(x,y,z) t += 0.2 # on incrémente t de 0.2
Variation de v
Ah… rage et désespoir. Cette formule toute compliquée ne fait qu'aligner des polyCubes? Oui et non. On a mis une valeur fixe à v afin de pouvoir lancer le script, hors il est lui aussi supposé prendre un certain nombre de valeurs dans son intervalle. Relançons le script avec d'autres valeurs de v : une figure se dessine. Ces alignement de cubes, définis en parcourant l'intervalle de t, correspondent donc aux droites transversales de notre ruban, et leur position sur le ruban est définie par v.
Variation de t
Faisons cette fois varier v sur son intervalle, avec des valeurs fixes de t :
import maya.cmds as mel from math import * t = 0 #valeur fixe de t v = 0 #valeur minimum de v while v <= pi : #valeur maximum de v # on calcule les coordonnées des points x = (2 + t * cos(v)) * cos(2 * v) y = (2 + t * cos(v)) * sin(2 * v) z = t * sin(v) # on place un polyCube selon ces coordonnées mel.polyCube(h=0.1, w=0.1, d=0.1) mel.move(x,y,z) v += 0.2 # on incrémente v de 0.2
On a cette fois les droites longitudinales de notre ruban, leur position sur le ruban se définissant par v :
C'est cela que nous manipulons lors du dépliage d'un modèle. Les coordonnées d'un point dans le référentiel d'une surface, ce sont ce que l'on nomme les UV.
Adopter v et t
Nous avons jusqu'ici une seule boucle, ce qui nous permet de parcourir une “ligne” de notre objet. Il nous faudrait maintenant parcourir toutes les lignes de notre objet, nous mettons donc toute notre première boucle dans une seconde :
import maya.cmds as mel from math import * # on parcours en long v = 0 #valeur minimum de v while v <= pi : #valeur maximum de v # on parcours en large t = -1.0 while t <= 1.0 : # on calcule les coordonnées des points x = (2 + t * cos(v)) * cos(2 * v) y = (2 + t * cos(v)) * sin(2 * v) z = t * sin(v) # on place un polyCube selon ces coordonnées mel.polyCube(h=0.1, w=0.1, d=0.1) mel.move(x, y, z) t += 0.2 # on incrémente t de 0.2 v += 0.2 # on incrémente v de 0.2
A chaque étape de la première boucle, une deuxième boucle est parcourue.
Autrement dit, pour chaque valeur que prend v, t prend une à une toutes les valeurs de son intervalle.
Autrement dit, à chaque étape du parcours longitudinal les points sont calculés transversalement.
Résolution
On a vu précédemment que l'on modifie le nombre de valeurs que prend v ou t dans leur boucle en changeant la valeur d'incrémentation. Et bien nous pouvons rapporter cela directement à notre objet 3D : plus ma valeur d'incrémentation sera faible plus j'aurais d'étapes, donc plus j'aurais de points calculés, donc plus j'aurais de polygones dans mon objet final ! Ces valeurs nous permettent donc de contrôler la résolution de l'objet longitudinalement et transversalement :
Des points aux courbes
C'est très joli cet ensemble de polyCubes, mais nous on veut un objet polygonal ! En effet ce serait dommage de s'arrêter quand on a fait les 3/4 du boulot, juste avant que cela ne devienne joli.
Nous avons des coordonnées de points dans l'espace, hors des points ça se relie (ben oui, un point, tout seul, ça sert à rien) pour faire une jolie courbe. En farfouillant la documentation Python/Mel, on se rend compte que Maya, avec la commande curve(), a la possibilité de créer une courbe à partir d'une liste de points !
Nous n'avons qu'une chose à faire : enregistrer nos points.
Enregistrer ses points
On va stocker les coordonnées de nos points dans un tableau, en se servant de la commande append(), qui ajoute la valeur donnée au tableau. On supprime aussi l'étape créant des polyCubes, qui ne servait qu'à vérifier que nos coordonnées étaient bonnes :
import maya.cmds as mel from math import * # on parcours en long v = 0 while v <= pi : points = [] #on initialise le tableau de points # on parcours en large t = -1.0 while t <= 1.0 : # on calcule les coordonnées des points x = (2 + t * cos(v)) * cos(2 * v) y = (2 + t * cos(v)) * sin(2 * v) z = t * sin(v) # on enregistre les coordonnées des points # on groupe les coordonnées dans une liste coords = (x, y, z) # on ajoute la liste au tableau de points points.append(coords) t += 0.2 # on affiche les tableaux de points pour vérifier print points v += 0.2
On a placé l'initialisation du tableau entre les deux boucles pour une raison précise : à chaque nouvelle tranche de la forme le tableau se réinitialise, permettant à une nouvelle liste de points de s'enregistrer. Ainsi nous créerons indépendamment chaque courbe.
Si on lance le script maintenant, on obtiens des dizaines de :
[(0.75170404445455141, 0.77398346766110715, -0.38941834230865052), (0.88004591930250731, 0.90612921048869477, -0.31153467384692046), (1.0083877941504631, 1.0382749533162823, -0.23365100538519035), (1.136729668998419, 1.1704206961438701, -0.15576733692346023), (1.2650715438463749, 1.3025664389714577, -0.077883668461730129), (1.3934134186943308, 1.4347121817990456, -2.1617060492121227e-017), (1.5217552935422867, 1.5668579246266332, 0.077883668461730088), (1.6500971683902423, 1.6990036674542208, 0.1557673369234602), (1.7784390432381985, 1.8311494102818089, 0.23365100538519029), (1.9067809180861544, 1.9632951531093965, 0.31153467384692046), (2.0351227929341102, 2.0954408959369841, 0.38941834230865052)]
C'est indigeste, ça semble chaotique, et pourtant si l'on regarde bien c'est tout à fait organisé :
[(x, y, z), (x, y, z), ...] [point1, point2, ...] courbe1 [(x, y, z), (x, y, z), ...] = [point1, point2, ...] = courbe2 [(x, y, z), (x, y, z), ...] [point1, point2, ...] courbe3
Chaque ligne définis une courbe, décrite par un ensemble de points, qui sont décrits par leurs coordonnées x, y et z.
Créer les courbes
Grâce au fait que l'on ait tout bien rangé, il va nous être très très simple de faire les courbes :
import maya.cmds as mel from math import * # on parcours en long v = 0 while v <= pi : points = [] # on parcours en large t = -1.0 while t <= 1.0 : # on calcule les coordonnées des points x = (2 + t * cos(v)) * cos(2 * v) y = (2 + t * cos(v)) * sin(2 * v) z = t * sin(v) # on enregistre les coordonnées des points coords = (x, y, z) points.append(coords) t += 0.2 # on crée une courbe à partir du tableau de points mel.curve(p=points) v += 0.2
Des courbes à la surface
En parcourant une nouvelle fois la documentation Python/Mel, on croise la commande loft() : “This command computes a skinned (lofted) surface passing through a number of NURBS curves”. Nous n'avons qu'à donner le nom de nos courbes à la fonction et on aura notre surface.
Pour cela il nous faut d'abord connaître le nom de toutes nos courbes, et les enregistrer dans un nouveau tableau. Une fois toutes les courbes créées et leurs noms stockés, il ne reste plus qu'à créer la forme finale et supprimer les courbes :
import maya.cmds as mel from math import * curves = [] # on initialise le tableau de courbes # on parcours en long v = 0 while v <= pi : points = [] # on parcours en large t = -1.0 while t <= 1.0 : # on calcule les coordonnées des points x = (2 + t * cos(v)) * cos(2 * v) y = (2 + t * cos(v)) * sin(2 * v) z = t * sin(v) # on enregistre les coordonnées des points coords = (x,y,z) points.append(coords) t += 0.2 # on crée une courbe à partir du tableau de points mel.curve(p=points) # on enregistre son nom dans le tableau de courbes # on liste ce qui est sélectionné (la dernière courbe créée) curveName = mel.ls(sl=True) # on enregistre le nom de la courbe dans le tableau curves.append(curveName[0]) v += 0.2 # on crée la surface à partir de la liste de courbes mel.loft(curves) # on crée la surface mel.delete(curves) # on supprime les courbes
Le fait que la surface soit ouverte est un problème de résolution de calcul. Plus votre résolution sera élevée (valeur d'incrémentation faible) plus la surface se rapprochera de ce qu'elle devrait être : fermée.
Il est néanmoins possible de tricher pour forcer la fermeture avec d'autres fonctions ou astuces.
Extrapolation
Certaines surfaces simples ne demandent par rapport à cette procédure qu'une modification des algorithmes de x, y et z. Vous pouvez même modifier l'algorithme à la main et, qui sait, vous trouverez peut-être la formule faisant un dragon ou une voiture en un clic.
Voila quelques formes intéressantes générées selon cette méthode :
Si vous avez des questions, des remarques, des suggestions, n'hésitez pas à m'en faire part.
~~DISCUSSION~~