Génération procédurale de réseaux logiques et des surfaces fermées résultantes par système de particules et analyse multi-dimensionnelle
Ce texte est une explication de l'algorithme mis en oeuvre pour générer de manière procédurale des réseaux logiques et les surfaces fermées résultantes au moyen de système de particules et d'analyse multi-dimensionnelle.
Vue d'ensemble
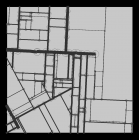
Le programme génère par un système de particules un ensemble de routes pseudo-aléatoires, détecte les croisements par un système de collision, et met ainsi en place un réseau de routes reliées par des noeuds. Le programme analyse ensuite ce réseau pour déterminer les polygones qu'il forme.
Structure du programme
La racine du programme, au plus simple, crée un monde d'une certaine taille, y ajoute quelques particules et le met à jour en boucle :
monde = Monde(500, 500)
monde.ajoute(5)
TANT QUE VOULU
monde.metAJour()
Monde
Le classe monde crée, stocke et manipule les particules, crée et édite la carte d'empreintes. Il peut être représenté par un rectangle (ou un cube) d'une certaine taille contenant géométriquement les autres éléments.
Membres
taille: vecteur définissant la taille du mondeparticulesVivantes: liste des particules activesparticulesMortes: liste des particules qui ne sont plus actives (archive)carteEmpreintes: tableau 2D d'empreintesfrequenceHistorique: fréquence à laquelle les particules doivent enregistrer leurs positions
Méthodes majeures
metAJour()
Trace le réseau tant qu'il y a des particules vivantes, puis génère les polygones.
SI nombre(particulesVivantes) > 0
traceReseau()
SINON
tracePolygones()
traceReseau()
Gère les évènements liés aux particules (naissance, mort, historique), la création des noeuds et la manipulation des empreintes.
POUR CHAQUE PARTICULE p
SI p est en dehors du monde
p.ajouteUnNoeud()
tue(p)
empreinte = recupereEmpreinte(p.position)
SI empreinte != null
p.ajouteUnNoeud(empreinte.particule, p.historique.taille)
empreinte.particule.ajouteUnNoeud(p, empreinte.index)
tue(p)
p.creeUneEmpreinte(p.historique.taille)
p.avance()
SI p.aAvance(frequenceHistorique)
p.ajouteUnNoeud()
chanceDeNaissance = (1 + p.facteurDeNaissance) * aleatoire()
SI chanceDeNaissance >= 1
donneNaissance(p)
donneNaissance(particule p)
Crée une nouvelle particule placée à côté de celle donnée, avec une direction perpendiculaire et un facteurDeNaissance un peu moins grand.
sens = randint(-1,0) * 2 + 1 // soit -1 soit 1 perpendiculaire.x = p.vitesse.y * sens perpendiculaire.y = p.vitesse.x * sens enfant = Particule() enfant.position = p.position + perpendiculaire enfant.vitesse = perpendiculaire enfant.facteurDeNaissance = p.facteurDeNaissance * 0.5 enfant.ajouteUnNoeud(p, 0) p.ajouteUnNoeud(enfant, p.historique.taille) ajoute(enfant)
Méthodes annexes
ajouter() : ajoute une particule par défaut aux particules vivantesajouter(nombre): ajoute un certain nombre de particules par défaut aux particules vivantesajouter(particule): ajoute la particule donnée aux particules vivantes
tuer(particule): déplace la particule donnée des particules vivantes vers les particules mortestuer(index): déplace la particule ayant l'index donné des particules vivantes vers les particules mortes
positionAleatoire(): retourne un vecteur position aléatoire à l'intérieur du mondevitesseAleatoire(): retourne un vecteur vitesse aléatoireestEnDehorsDuMonde(particule): indique si la particule donnée est à l'extérieur du monde
recupereEmpreinte(position): retourne l'empreinte présente à la position donnéecreeUneEmpreinte(particule, index): crée une empreinte de la particule donnée à sa position courante avec l'index donné
Particule
Les particules sont des objets contenus dans le monde ayant principalement une position et une vitesse, pouvant ainsi se déplacer. Chaque particule stocke un historique de ses positions, permettant de recréer son cheminement.
Membres
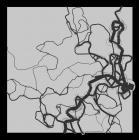
position: vecteur de coordonnéesdirection: vecteur directionneldistanceParcouruehistorique: liste de noeuds correspondant à son tracéfacteurDeNaissance: chance qu'elle a -à tout moment- d'enfanter. Correspond aussi à l'importance du tracéfacteurDeVariation: intensité de variation de sa direction. Permet de définir différent profils, comme “aller tout droit” avec 0 ou “spaghetti” avec 0.5
Méthodes majeures
avance()
Modifie la direction de la particule selon son facteurDeVariation et un peu d'aléatoire :
variation.x = aleatoire(-1,1) variation.y = aleatoire(-1,1) variation = variance * facteurDeVariation direction = normalise(direction + variation)
Modifie la position selon la direction…
position = position + direction
…et augmente la distanceParcourue :
distanceParcourue = distanceParcourue + 1
Méthodes annexes
aParcouru(distance): indique si la distanceParcourue est supérieure à la distance donnéeajouterUnNoeud(): ajoute à l'historique un noeud relatif à la position courante puis remet la distanceParcourue à zéroajouterUnNoeud(particule): ajoute à l'historique un noeud relatif à la position courante et la particule donnée et remet la distanceParcourue à zéroajouterUnNoeud(position, particule, index): ajoute à l'historique un noeud relatif à la position, la particule et l'index donnés et remet la distanceParcourue à zéro
Empreinte
Classe (ou structure) rassemblant une référence à une particule et un index. La référence à la particule peut être nulle.
Noeud
Classe (ou structure) rassemblant une position, une référence à une particule et un index. La référence à la particule peut être nulle.
Problématiques majeures
Génération de routes
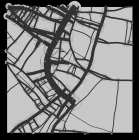
Afin d'obtenir un réseau réaliste de façon dynamique, l'algorithme génère des particules qui évoluent en fonction de variables données. Celles-ci permettent de contrôler leur manière de se déplacer et ainsi obtenir différent profils de réseaux.
Régulièrement, les particules enregistrent leur position. L'ensemble de ces positions représente ainsi leur parcourt.
A tout moment une particule peut donner naissance à une autre, qui pourra faire de même avec une probabilité légèrement réduite.
Détection des collisions
Pour détecter les collisions entre deux tracés il faut pouvoir déterminer à chaque instant si une particule traverse le chemin emprunté par une autre.
Il existe au moins deux grande méthodes : par une analyse purement géométrique ou par traitement d'image. La première, bien que précise, se révèle très lourde à calculer quand la seconde nécessite généralement des bibliothèques graphiques.
Il a été choisi de se servir d'un tableau à deux dimensions de la taille du monde, ce qui permet aux index des cases d'être interprétés géométriquement. Une particule située à une certaine position peut ainsi vérifier le contenu de la case correspondante.
A chaque fois qu'une particule découvre une nouvelle case, elle y laisse une empreinte. La particule suivante arrivant sur cette même case pourra déduire qu'une autre y est déjà passée et laquelle.
La précision de cette méthode dépend donc de la grandeur du tableau.
Réseau nodal
A chaque collisions, les deux particules insèrent un noeud à la bonne place dans leur historique. Ce noeud contient une référence à la particule rencontrée et la position de la dite rencontre. Ces noeuds font le lien entre les différents tracés, dessinant ainsi le réseau.
Génération de polygones
A partir des espaces fermés du réseau, on peut former des polygones. Pour cela, on parcourt l'historique de chaque particule jusqu'à trouver un noeud de croisement. Si le tracé rencontré peut être suivi sur la droite, on continue de former le polygone le long de ce dernier. Si ce n'est pas le cas, la création du polygone continue sur le même tracé. De cette manière, tous les espaces formés par le réseau sont couverts.
On obtient ainsi une structure géométrique logique pouvant servir de base à la modélisation d'une ville en assimilant les tracées à des voies de circulations, les noeuds à des carrefours et les polygones à des zones de construction.