articles:mel-python:animation

Table des matières

L'animation procédurale

L'animation procédurale

Introduction

Le but est, au moyen d'un exemple simple, le rebond d'une balle, nous semblant aujourd'hui évident, de comprendre en partie le déroulement mathématique, physique ou algorithmique à la base de l'animation procédurale.

“En synthèse d'image numérique, l'animation procédurale est une animation d'objets virtuels par génération en temps réel de mouvements, selon un ensemble de règles procédurales. L'animateur 3D spécifie les règles (par exemple des lois du monde physique décrites par des relations mathématiques), et les conditions initiales avant de lancer la simulation.” Cf. Wikipedia

Je rajouterais que l'intérêt majeur de l'animation procédurale est la génération de schémas complexes - voir très complexes - à partir d'outils et règles simples, voir très simples.

Key frames

En animation par key frames nous définissons la valeur d'un attribut à différents temps, et le logiciel interpole cette valeur entre les clés.

Position en Y de la balle au cours du temps. Cinq clés ont été placées et la courbe a été modelée pour mimer le rebond d'une balle.

Dynamics

En animation procédurale rien de tout cela. Nous définissons les conditions initiales en plaçant des objets dans l'espace et en définissant leurs propriétés, ainsi que les règles de la simulation en ajoutant des forces ou des conditions :

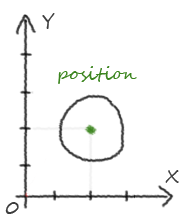
Préparation d'une simulation dynamique sous maya.

Dans l'illustration ci-dessus, les conditions initiales sont :

Il existe un objet ayant une certaine forme (sphérique), une certaine position, une certaine taille et une vitesse nulle.
Il existe un objet ayant une certaine forme (cubique), une certaine position, une certaine taille et une vitesse nulle.

Les règles sont :

La sphère peut se déplacer (active rigid body).
Le cube ne peut pas se déplacer (passive rigid body).
Une force de gravité (gravity field) affecte la sphère (affect selected objects).
Si deux Rigid body se rencontrent il y a collision et ils réagissent en conséquence (règle intrinsèque aux rigid body)

Lorsque nous lançons la simulation, la sphère chute et rebondis sur le cube.

De par les conditions et les règles nous comprenons pourquoi, toute la question est désormais : comment?

Pour comprendre comment cela fonctionne, nous allons programmer l'animation dynamique de notre balle en partant de zéro.

Les vecteurs

L'animation procédurale nécessite la maitrise d'un objet mathématique merveilleux : le vecteur.

Avant d'aller plus loin, je vous conseille donc fortement de lire l'article sur Les vecteurs.

Conditions initiales

Une fois les vecteurs assimilés, l'animation procédurale n'aura plus de secrets pour vous. Et cela tombe bien car on passe à la pratique, avec Maya et son Script Editor.

Les conditions initiales pour avoir une balle qui rebondis sont… suspense…

Avoir une balle ayant une certaine taille, une certaine position et une certaine vitesse.

Normalement cela ne devrait pas poser de problèmes, c'est des chose que nous savons faire.

Première mission : se procurer une balle

Hop, une balle.

# on importe le module maya.cmds
from maya.cmds import *
 
# on définis une taille
taille = 5
# et on définis que notre balle
# est une sphère de cette taille
balle = polySphere(radius=taille)

Deuxième mission : donner une position initiale à notre balle

Le vecteur position de notre balle indique sa position dans l'espace.

Maintenant que l'on a les vecteurs dans la poche, plus question de faire ça :

position_x = 0
position_y = 50
position_z = 0

Maintenant on fait :

position = [0, 50, 0]  # position de départ

Notre variable position est donc un vecteur de coordonnées, indiquant une position dans l'espace.

Troisième mission : donner une vitesse initiale à notre balle

Le vecteur vitesse de notre balle représente une force physique dirigée.

Nous pourrions faire :

vitesse = 1

Et nous aurions une valeur de vitesse générale. Mais regardez ce qu'apportent ici les vecteurs :

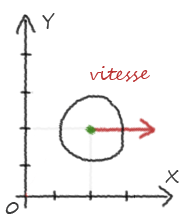
vitesse = [1, 0, 0]  # vitesse de départ

Notre variable vitesse est ici un vecteur directionnel indiquant à la fois la direction, le sens, et l'intensité de notre vitesse dans l'espace! En plus d'être d'une “intensité” de 1 (la longueur de notre vecteur), notre vitesse est ici dirigée vers la droite. C'est la représentation mathématique d'une force physique.

Débriefing

from maya.cmds import *
 
# conditions initiales
taille = 5
balle = polySphere(radius=taille)
position = [0, 50, 0]
vitesse = [1, 0, 0]

Très bien, mais si on lance notre code, à part créer une balle il ne se passe rien. Normal, il n'y a encore aucune notion de mouvement.

Animation

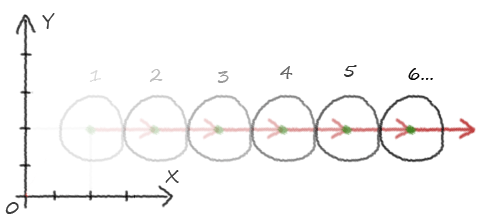
Mouvement

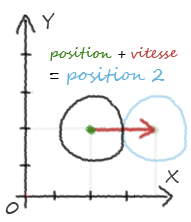
Le vecteur vitesse nous indique donc vers où doit se diriger notre balle. Il faut que notre balle se déplace de sa position à… sa position plus sa vitesse. Il nous suffit d'ajouter au vecteur position le vecteur vitesse. Pour cela on utilise la fonction précédemment citée.

nouvelle position = position vitesse

from maya.cmds import *
 
# fonctions
def vectorAdd(a, b):
	return [a[0] b[0], a[1] b[1], a[2] b[2]]
 
# conditions initiales
taille = 5
balle = polySphere(radius=taille)
position = [0, 50, 0]
vitesse = [1, 0, 0]
 
# mouvement
print position # on affiche la position avant
# on change la position selon la vitesse
position = vectorAdd(position, vitesse)
print position # on affiche la position après
# et on déplace la balle
move(position[0], position[1], position[2],balle)

Résultat :

[0, 50, 0]
[1, 50, 0]

La balle a bien avancé sur la droite, comme indiqué par le vecteur vitesse, par contre elle ne l'a fait qu'une fois, quand on a lancé le script. Pour visualiser un mouvement, il faut répéter cette opération 20, 30 fois par secondes. Et pour cela nous n'avons qu'à mettre le calcul du mouvement dans une boucle.

Boucle

A la suite des conditions initiales, faisons une boucle :

from maya.cmds import *
 
# fonctions
def vectorAdd(a, b):
	return [a[0]+b[0], a[1]+b[1], a[2]+b[2]]
 
# conditions initiales
taille = 5
balle = polySphere(radius=taille)
position = [0, 50, 0]
vitesse = [1, 0, 0]
 
# animation
time = 300 # Durée de l'animation en frame (nombre de tour de la boucle)
# Pour chaque frame de l'animation...
for frame in range(1, time):
	# On place la timeline à la frame actuelle (cela permet 
	# d'actualiser le viewport et donc de voir l'animation)
	currentTime(frame)
 
	# mouvement
	position = vectorAdd(position, vitesse)
	move(position[0], position[1], position[2], balle)

Et voila une superbe simulation de balle dans le vide!

Mouvement de la balle répété par une boucle.

Règles d'environnement

Nous avons la base fonctionnelle de notre simulation, nous pouvons désormais définir des règles permettant de décrire l'environnement de la simulation. Dans l'exemple de la balle qui rebondis nous allons mimer certaines lois physiques, mais il est possible de tout imaginer.

Que se passe-t-il concrètement quand une balle rebondis? Elle se dirige vers le sol, change de direction à son contact puis peu à peu s'y re-dirige, change de direction à son contact, etc…

Forces

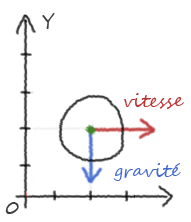
Si la balle se dirige vers le sol, c'est que quelque chose l'y pousse : la gravité.

Qu'est-ce que la gravité? Cela a l'air d'une question idiote, mais la réponse peut ne pas l'être. Car si l'on observe en infiniment grand la théorie de la relativité générale nous parle d'une “manifestation de la déformation de la géométrie de l'espace-temps sous l'influence des objets qui l'occupent”, alors qu'en infiniment petit les théories quantiques de la gravitation nous disent que “l'équation des ondes gravitationnelles peut s'interpréter comme celle de la propagation d'une particule”. A notre échelle cela sera heureusement plus simple : c'est une force dirigée vers le bas.

Créer une force

Ajout d'une force.

Une force dirigée, comme notre vitesse, on sait que cela se représente simplement avec un vecteur directionnel. Pour définir une nouvelle force, après les conditions initiales nous n'avons donc qu'à faire :

# la gravité est seulement
# une force dirigée vers le bas
gravité = [0, -0.1, 0]

Appliquer une force

Calcul de la résultante des forces.

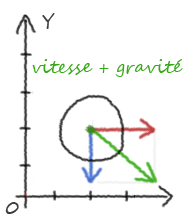
La direction de notre objet doit maintenant dépendre de plusieurs forces : sa direction préalable plus la gravité. Pour qu'une force affecte un objet, il suffit donc de l'ajouter au vecteur directionnel. On dit que le vecteur vitesse de l'objet est la résultante des forces qui lui sont appliquées.

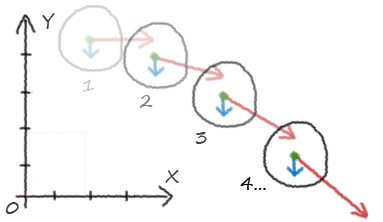
from maya.cmds import *
 
# fonctions
def vectorAdd(a, b):
	return [a[0] b[0], a[1] b[1], a[2] b[2]]
 
# conditions initiales
taille = 5
balle = polySphere(radius=taille)
position = [0, 50, 0]
vitesse = [1, 0, 0]
 
# environnement
gravite = [0, -0.1, 0]
 
# animation
time = 100
for frame in range(1, time):
    currentTime(frame)
 
    # regles
    vitesse = vectorAdd(vitesse, gravite)
 
    # mouvement
    position = vectorAdd(position, vitesse)
    move(position[0], position[1], position[2], balle)

La direction de la balle est la résultante de différente forces.

Rien de plus simple, non? En deux lignes, nous pouvons rajouter une force dirigée dans n'importe quel sens (une gravité vers le haut, pourquoi pas) et de n'importe quelle intensité (une gravité divisée par dix, et voila la lune).

Rebond

Nous allons maintenant faire rebondir la balle lorsqu'elle touche le sol.

Contact

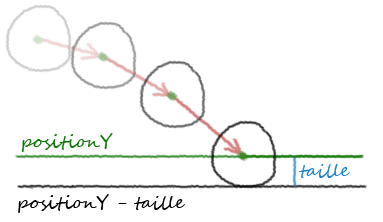
Disons que le sol est horizontal, à une certaine hauteur. La balle touche alors le sol si sa position en Y moins sa taille est inférieure ou égale à la hauteur du sol, et dans ce cas la balle ne chute pas. Faisons donc une condition pour nos règles :

	# regles
	# si la position de la balle en Y moins sa taille
	# est inférieure ou égale à la hauteur du sol
	if position[1] - taille <= sol:
		# il y a contact, la balle ne chute pas
		vitesse = [0, 0, 0] # on stoppe sa vitesse
	else: # sinon la balle chute
		vitesse = vectorAdd(vitesse, gravite)

La balle chute, et une fois… dans le sol, s'arrête. Notre condition vérifie si la balle est déjà en contact ou dans le sol, il est donc un peu trop tard pour réagir. Pour palier à cela, nous allons vérifier si la balle serait dans le sol à la frame suivante si elle continuait sa course.

	# regles
	# On calcule la prochaine position de la balle
	nextPosition = vectorAdd(position, vitesse)
	# si la prochaine position de la balle en Y moins sa taille
	# est inférieure ou égale à la hauteur du sol
	if nextPosition[1] - taille <= sol:
		# il y a contact, la balle ne chute pas
		vitesse = [0, 0, 0] # on stoppe sa vitesse
	else: # sinon la balle peut en effet chuter
		vitesse = vectorAdd(vitesse, gravite)

La balle touche le sol si sa position plus sa taille est au niveau du sol.

Réaction

Le contact entre la balle et le sol entraîne une force de réaction.

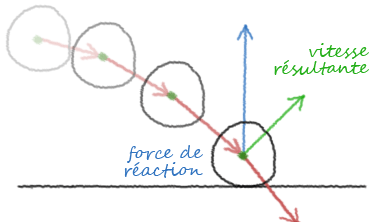
Lorsque la balle touche le sol, de par son élasticité et parce qu'elle ne peut traverser ce dernier, elle s'écrase. Une fraction de seconde plus tard, tentant de retrouver sa forme originale, elle est propulsée vers le haut. Ceci se représente par une force de réaction, perpendiculaire à la surface de contact.

Dans notre cas la force de réaction est verticale et correspond à :

[0, -vitesse[1] * 2, 0]

Dans notre condition, quand nous savons que la balle touche le sol, au lieu de la stopper nous allons calculer cette force de réaction et l'ajouter à la vitesse :

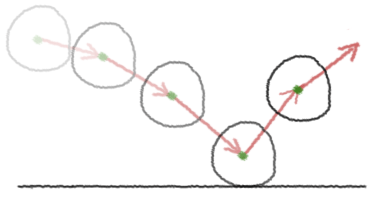
	# regles
	nextPosition = vectorAdd(position, vitesse)
	if nextPosition[1] - taille <= sol:
		# il y a contact et se crée une force de réaction
		reaction = [0, -vitesse[1] * 2, 0]
		# qui s'ajoute au vecteur vitesse
		vitesse = vectorAdd(vitesse, reaction)
	else: # sinon la balle peut en effet chuter
		vitesse = vectorAdd(vitesse, gravite)

Et voila notre balle qui rebondis!

La condition permet de passer ponctuellement d'une force de gravité à une force de réaction, entraînant le rebond.

Efficience

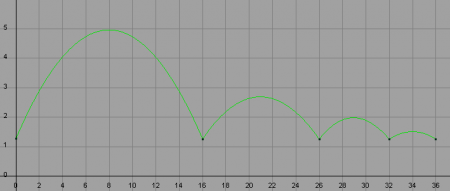
Vous pouvez remarquer que quel que soit le nombre de rebonds effectué par la balle, jamais elle ne s'arrête. Nous avons en effet créé ici une balle rebondissante parfaite, qui à chaque rebond remonte exactement aussi haut qu'au départ, sans jamais s'essouffler.

Pour changer cela il n'y a qu'à modifier l'intensité de la force de réaction.

L'efficience du rebond d'une matière étant un réel paramètre de description physique (en anglais “bounciness”), si l'on veut être plus précis cela correspond à :

	# regles
	nextPosition = vectorAdd(position, vitesse)
	if nextPosition[1] - taille <= sol: # rebond
		bounciness = 0.75
		reaction = [0, -vitesse[1] * (1 + bounciness), 0]
		vitesse = vectorAdd(vitesse, reaction)
	else: # chute
		vitesse = vectorAdd(vitesse, gravite)

Quelques indications :

0.0 : rebond nul, l'objet ne rebondis pas.
0.3 : rebond réaliste peu efficient, chaque rebond est beaucoup plus faible que le précédent (type boule de bowling)
0.7 : rebond réaliste efficient (type ballon de foot)
0.9 : rebond réaliste très efficient, chaque rebond est presque aussi important que le précédent (type balle rebondissante)
1.0 : rebond parfait, chaque rebond est aussi important que le précédent (mouvement perpétuel)
>1 : rebond irréaliste, chaque rebond est plus important que le précédent (type flubber)

Invalid Link

Efficience du rebond de quelques types de balles.

Friction

Si maintenant la taille du rebond décroit avec le temps, le mouvement de la balle initié par la force de départ est lui toujours perpétuel : même sans rebondir, elle continue de glisser sur le sol. Il nous manque un paramètre de friction. L'effet de la friction est de freiner un objet lorsqu'il y a contact. Qui dit freiner dit diminuer sa vitesse.

Il nous faut donc réduire la longueur du vecteur vitesse quand il y a contact avec le sol. Comme vu dans le chapitre sur les vecteurs, il s'agit d'une simple multiplication du vecteur avec un nombre. Je récupère donc la fonction à cet effet :

def vectorMult(a, b):
	return [a[0]*b, a[1]*b, a[2]*b]

Dans notre condition, après avoir calculé la force de réaction et la nouvelle vitesse, nous n'avons plus qu'à multiplier cette dernière :

	# regles
	nextPosition = vectorAdd(position, vitesse)
	if nextPosition[1] - taille <= sol: # rebond
		bounciness = 0.75
		friction = 0.95
		reaction = [0, -vitesse[1] * (1 + bounciness), 0]
		vitesse = vectorAdd(vitesse, reaction)
		vitesse = vectorMult(vitesse, friction)
	else: # chute
		vitesse = vectorAdd(vitesse, gravite)

Quelques indications :

0.00 : friction maximale, l'objet est immédiatement stoppé au contact de la surface.
0.25 : friction réaliste forte, l'objet est très vite freiné par la surface (type sable)
0.99 : friction réaliste faible, l'objet est lentement freinée par la surface (type de sol lisse)
1.00 : friction nulle, l'objet n'est pas freiné par la surface (type glace)
>1.00 : friction irréaliste, l'objet est accéléré par la surface (type accélérateur de jeu de course)

Code final

from maya.cmds import polySphere, currentTime, move
 
# fonctions
def vectorAdd(a, b):
	'''Somme de deux vecteurs'''
	return [a[0] + b[0], a[1] + b[1], a[2] + b[2]]
def vectorMult(a, b):
	'''Multiplication de vecteur par un nombre'''
	return [a[0] * b, a[1] * b, a[2] * b]
 
# conditions initiales
taille = 5
balle = polySphere(radius=taille)
position = [0, 50, 0]
vitesse = [1, 0, 0]
bounciness = 0.75
friction = 0.95
 
# environnement
gravite = [0, -0.1, 0]
sol = 0
 
# animation
time = 100
for frame in range(1, time):	
	# regles
	positionGravite = vectorAdd(position, vitesse)
	if positionGravite[1] - taille <= sol: # rebond
		reaction = [0, -vitesse[1] * (1 + bounciness), 0]
		vitesse = vectorAdd(vitesse, reaction)
		vitesse = vectorMult(vitesse, friction)
	else: # chute
		vitesse = vectorAdd(vitesse, gravite)
 
	# mouvement
	position = vectorAdd(position, vitesse)
	currentTime(frame)
	move(position[0], position[1], position[2], balle)

Conclusion

Vous remarquerez que l'on utilise seulement trois fonctions de Maya : polySphere, currentTime et move, qui servent uniquement à visualiser le résultat de nos calculs. Cette procédure est donc transposable à tout langage, tout logiciel permettant de programmer (Flash, Processing, Blender…) et n'est en rien rattaché à Maya. Il s'avère par la même occasion que les temps de calculs sont infiniment plus rapides que si l'on avait usé et abusé des fonctions internes au logiciel.

Voila, j'espère vous avoir fait découvrir deux ou trois choses ;) .

A venir, peut-être

Version orientée objet.
Corps mous, surfaces flexibles, systèmes de particules, animation comportementale, algos génétiques, fractales…
Ouverture sur d'autres logiciels (Blender?), d'autres langages (Processing?).

Si vous avez des questions, des remarques, des suggestions, n'hésitez pas à m'en faire part.

~~DISCUSSION~~