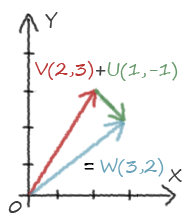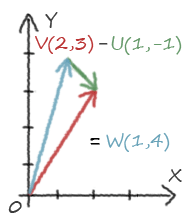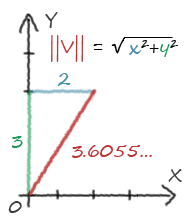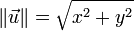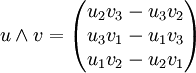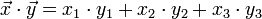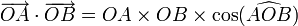Table des matières
Les vecteurs
Comprendre les vecteurs
Je survole rapidement les points important, le but n'est pas de devenir mathématicien mais d'en comprendre suffisamment pour pouvoir s'en servir sans souffrir.
Un quoi?
Un vecteur est simplement une liste de valeurs :
(18, -1, 12.5, 0.001) (0, 16)
Il sert simplement à représenter… quelque chose qui se décrit avec plusieurs valeurs!
Vecteur de coordonnée
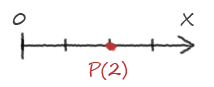
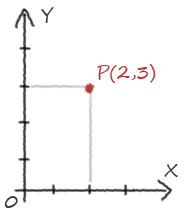
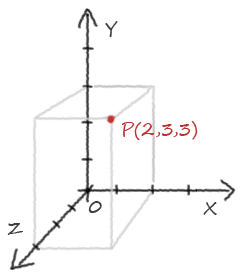
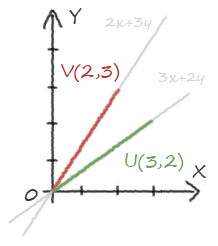
Un vecteur peut décrire une position dans l'espace, on le nomme alors simplement vecteur de coordonnées ou… point.
Puisqu'un dessin vaut plus qu'un long discours :
Vecteur directionnel
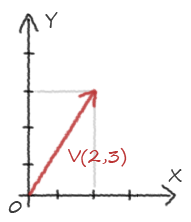
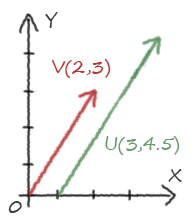
Un vecteur peut aussi décrire un déplacement, on le nomme alors vecteur directionnel. On ne traduit simplement plus le vecteur comme le fait d'être une position, mais comme le déplacement effectué pour aller à cette position. On peut ainsi définir qu'un vecteur (1,2,-1) correspond à “avancer d'un en x, puis avancer de deux en y, puis reculer d'un en z”. Un vecteur directionnel indique ainsi à la fois une direction, un sens et une longueur. Cf Vecteur: approche géométrique
En dessin :
Créer des vecteurs
En programmation on utilise généralement un tableau pour définir un vecteur, car c'est une structure de données simple, présente dans tout langage :
# création d'un vecteur position = [1.5, 5, -3] # affichage de ses valeurs print position[0] # première valeur du tableau : 1.5 print position[1] # deuxième valeur du tableau : 5 print position[2] # troisième valeur du tableau : -3
Python propose néanmoins d'autres structures de données pouvant servir à faire des vecteurs :
Les dictionnaires
Rappel : un dictionnaire est semblable à un tableau, mais permet d'utiliser des index maison : au lieu d'avoir tab[2], nous pouvons avoir tab['tomate'].
# création d'un vecteur position = {'x':1.5, 'y':5, 'z':-3} # affichage de ses valeurs print position['x'] # valeur ayant pour index 'x' : 1.5 print position['y'] # valeur ayant pour index 'y' : 5 print position['z'] # valeur ayant pour index 'z' : -3
C'est plus lisible, mais beaucoup plus lourd à calculer qu'un tableau pour python. Beaucoup trop pour être utilisé comme vecteur.
Les tuples, ou listes
Rappel : un tuple est semblable à un tableau, à la différence qu'une fois qu'il est créé, on ne peut en modifier le contenu.
# création d'un vecteur position = (1.5, 5, -3) # affichage de ses valeurs print position[0] # première valeur du tuple : 1.5 print position[1] # deuxième valeur du tuple : 5 print position[2] # troisième valeur du tuple : -3
C'est beaucoup plus rapide à calculer pour python qu'un tableau, mais un vecteur étant généralement modifié au cours d'un programme cela ne nous servira pas à grand chose.
Les classes
En programmation orientée objet, il semble évident d'utiliser une classe vecteur. Beaucoup plus simple d'utilisation, plus rapide, avec ses propres méthodes, surcharges d'opérateurs, etc…
Pour l'anecdote j'ai découvert l'intérêt de la programmation orientée objet en me faisant ma classe vecteur en python :p
Classe qui se présenterait par exemple ainsi :
class Vector(): # initialisation def __init__(self, x=0, y=0, z=0): self.x, self.y, self.z = x, y, z # surcharges def __add__(a, b): return Vector(a.x + b.x, a.y + b.y, a.z + b.z) # ... # méthodes def norm(self): return sqrt(self.x**2 + self.y**2 + self.z**2) def crossProduct(self, b): x = self.y * b.z - self.z * b.y y = self.z * b.x - self.x * b.z z = self.x * b.y - self.y * b.x return Vector(x, y, z) # ...
Et s'utiliserait ainsi :
# instanciation d'un vecteur position = Vector(1.5, 5, -3) # affichage de ses valeurs print position.x # valeur de l'attribut x de l'instance : 1.5 print position.y # valeur de l'attribut y de l'instance : 5 print position.y # valeur de l'attribut z de l'instance : -3
Manipuler des vecteurs
Quelques opérations sont nécessaire pour pouvoir utiliser les vecteurs.
Pour une balle qui rebondis l'addition, la soustraction et la multiplication suffisent, pas la peine de voir le reste. Pour aller plus loin la norme, le produit vectoriel et le produit scalaire sont utiles, voir nécessaires.
Addition, soustraction, multiplication
On a constamment besoin d'additionner ou de soustraire des vecteurs entre eux, ou de les multiplier par un nombre.
L'addition de deux vecteurs u et v est un vecteur w dont chaque membres est la somme des membres de u et v correspondant :
u(x, y, z) + v(x, y, z) = w(ux+vx, uy+vy, uz+vz)
La soustraction de deux vecteurs u et v est un vecteur w dont chaque membres est la soustraction des membres de u et v correspondant :
u(x, y, z) - v(x, y, z) = w(ux-vx, uy-vy, uz-vz)
La multiplication d'un vecteur u par une valeur a est un vecteur w dont chaque membre est la multiplication du membre correspondant de v par a :
u(x, y, z) * a = w(ux*a, uy*a, uz*a)
En python
# on définis deux vecteurs u = [3, -1, 2] v = [1, 5, -3] a = 2 # w = u + v w = [u[0] + v[0], u[1] + v[1], u[2] + v[2]] # w = u - v w = [u[0] - v[0], u[1] - v[1], u[2] - v[2]] # w = u * a w = [u[0] * a, u[1] * a, u[2] * a
Comme toute procédure qui pourra être utilisée plusieurs fois dans un programme, il est utile d'en faire des fonctions :
# définition des fonctions def vectorAdd(a, b): return [a[0]+b[0], a[1]+b[1], a[2]+b[2]] def vectorSub(a, b): return [a[0]-b[0], a[1]-b[1], a[2]-b[2]] def vectorMult(a, b): return [a[0]*b, a[1]*b, a[2]*b # utilisation u = [3, -1, 2] v = [1, 5, -3] a = 2 w = vectorAdd(u, v) # (4, 4,-1) w = vectorSub(u, v) # (2, -6, 5) w = vectorMult(u, a) # (6, -2, 4)
On comprend quand même mieux
w = vectorAdd(u, v)
Que
w = [u[0] + v[0], u[1] + v[1], u[2] + v[2]]
Non?
Norme
Oulala, qu'est-ce que c'est que ça?
Ces doubles barres entourant le vecteur font référence à sa norme. Et la norme d'un vecteur, c'est tout simplement sa longueur. Et pour calculer sa longueur rien de plus simple, on appelle Pythagore.
Pythagore!
| Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit. |
Le triangle est rectangle car le repère est orthogonal, les longueurs des côtés sont les composantes (x,y,etc…) du vecteur, on a donc immédiatement notre longueur.
En python
# la racine carrée est dans le module math from math import sqrt # définition de la fonction def vectorNorm(a): # puissance de 2 s'écrit "**2" return sqrt(a[0]**2 + a[1]**2 + a[2]**2) # utilisation u = [3, -1, 2] norme = vectorNorm(u)
Produit vectoriel
Le produit vectoriel de deux vecteurs U et V, écrit U ^ V, correspond à un vecteur W perpendiculaire au plan contenant les deux vecteurs U et V.
Il se nomme en anglais cross product et s'écrit U x V.
Une autre définition du produit vectoriel fait apparaitre le sinus de l'angle entre les deux vecteurs :
En python
# définition de fonction def crossProduct(a, b): x = a[1] * b[2] - a[2] * b[1] y = a[2] * b[0] - a[0] * b[2] z = a[0] * b[1] - a[1] * b[0] return [x, y, z] # utilisation u = [3, -1, 2] v = [1, 5, -3] w = crossProduct(u, v) # (-7, 11, 16)
Produit scalaire
Le produit scalaire de deux vecteurs U et V s'écrit U . V. Il se nomme en anglais dot product.
Une autre définition du produit vectoriel fait apparaitre le cosinus de l'angle entre les deux vecteurs :
En python
# définition de fonction def dotProduct(a, b): return a[0] * b[0] + a[1] * b[1] + a[2] * b[2] # utilisation u = [3, -1, 2] v = [1, 5, -3] w = dotProduct(u, v) # -8
~~DISCUSSION~~